Il modello di Poincarè

Per renderci meglio conto della geometria iperbolica analizzeremo il modello di Poincarè (1854-1912). Poincaré, nel suo libro La scienza e l'ipotesi del 1902, presentò il suo modello sotto forma di racconto di fantasia; mantenere questa impostazione ci libererà dalla necessità di appesantire la trattazione con la discussione di aspetti tecnici. Il vero modello di Poincarè è apparentemente diverso ma in realtà equivalente a quello che esporrò.

Sia dato in un piano euclideo un cerchio euclideo C di raggio R, immaginiamo che all'interno di questo cerchio viva una popolazione di esseri bidimensionali che noi osserveremo da fuori. All'interno di C avviene uno strano fenomeno che provoca la contrazione dei campioni di lunghezza (regoli che quando sono al centro di C misurano un metro) man mano che si allontanano dal centro. La formula che descrive quantitativamente questo fenomeno è: lunghezza di un regolo campione a distanza r dal centro =1- r²/R²metri, dove r è misurata a partire dal punto medio del regolo stesso. Se poniamo il regolo al centro (r = 0), poi lo allontaniamo procedendo verso il bordo osservandolo a metà strada (r = ½ R), a tre quarti (r = ¾ R), e così via.

Supponiamo inoltre che ogni cosa all'interno di C (compresi gli esseri che ci vivono) subisca una corrispondente variazione delle dimensioni lineari, cosicché nessun abitante di questo strano mondo possa accorgersi del fenomeno. Solo noi che osserviamo da fuori ci accorgiamo che l'omino rimpicciolisce allontanandosi dal centro, e con lui rimpiccioliscono tutte le cose che lo circondano.

Supponiamo infine che il fenomeno che caratterizza C costringa ai raggi di luce che si propagano tra due punti interni al cerchio a seguire sempre il percorso più breve, se misurato nel sistema di misura degli abitanti di C.

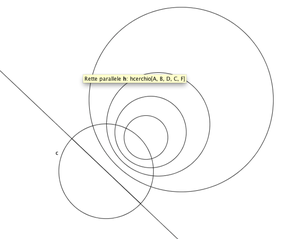
Al nostro punto di vista, un raggio di luce che unisce due punti sarà dritto solo se i due punti sono su un diametro di C; altrimenti presenterà una convessità rivolta verso il centro, poiché i regoli di misura si allungano andando in quella direzione. È possibile dimostrare che questi cammini curvi sono archi di circonferenze "ortogonali" a C, cioè archi di circonferenze che incontrano C in modo tale che nei punti di intersezione le rispettive tangenti siano perpendicolari fra loro.

Gli abitanti di C non si renderanno conto di vivere all'interno di un cerchio: per quante volte riportino consecutivamente un metro lungo quello che noi sappiamo essere un diametro del cerchio, non raggiungeranno mai il bordo, perché il metro si accorcia troppo velocemente.

Vicino al bordo la lunghezza di un regolo, così come ogni altra lunghezza, si avvicina al valore: 1- r²/R² = 0. Per ricoprire la distanza che li separa dal bordo, di regoli infinitesimi, ma per loro sempre uguali, ne occorreranno sempre più.
Dunque, per coloro che vivono al suo interno, il cerchio C si estende all'infinito in tutte le direzioni, e costituisce il "piano". Gli abitanti di C intenderanno per "linea retta" il percorso di un raggio di luce o il percorso più breve tra due punti, e poiché all'interno di C queste due nozioni sono equivalenti, in ogni caso, le linee rette sono per loro quelle che noi vediamo come parti interne di diametri di C o di archi di circonferenze ortogonali a C. Siccome i raggi di luce all'interno di C seguono esattamente questi percorsi, ciascuna linea disegnata in azzurro in figura apparirà rettilinea ad un osservatore che guardi lungo di essa. Gli abitanti di questo strano mondo accetteranno che per un punto esterno ad una retta ci sarà più di una retta parallela. Infatti dati A e B che giacciono su un diametro, le parallele asintotiche ad AB per P saranno due archi di cerchio ortogonali YPZ e WPX passanti per gli estremi Y* e X* del diametro (osserviamo che questi punti stanno su C, dunque per gli abitanti non esistono, per loro il cerchio non ha bordo).