Euclide emendato da ogni neo
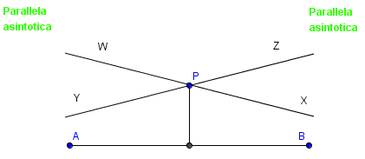
Lo sforzo più significativo di questo tipo fu compiuto da Gerolamo Saccheri, un gesuita professore all’università di Pavia, che può essere considerato come un precursore di entrambe le geometrie non euclidee successivamente scoperte: la geometria ellittica e quella iperbolica. Saccheri, nella sua opera intitolata “Euclide emendato da ogni neo, ossia tentativo geometrico col quale si stabiliscono gli stessi primi principi di geometria universale”, prende le mosse dalla considerazione di una figura fondamentale, il quadrilatero birettangolo isoscele. Poi prende in esame tre ipotesi relative dei due angoli al vertice che sono entrambi retti, o acuti o ottusi. Saccheri cerca di confutare l’ipotesi dell’angolo acuto, dopo aver confutato quella dell'angolo ottuso. In questa ipotesi per un punto esterno alla retta data passano due rette asintotiche che dividono le rette del fascio in due classi; alla prima appartengono quelle rette del fascio che incontrano la retta data, alla seconda quelle che hanno con essa una perpendicolare comune. Le parallele asintotiche si avvicinano l’una all’altra nella direzione del parallelismo. Il ragionamento di Saccheri, finora assai rigoroso, slitta su un piano intuitivo e di puro convincimento psicologico quando trasferisce all’infinito concetti e considerazioni validi per enti posti a distanza finita, per dimostrare che l’ipotesi dell’angolo acuto è assolutamente falsa “ perché ripugna alla natura della retta”.
 Laboratorio Piano Lauree Scientifiche
Geometrie non Euclidee
Centro Educativo Ignaziano
Palermo
Laboratorio Piano Lauree Scientifiche
Geometrie non Euclidee
Centro Educativo Ignaziano
Palermo
