Concetti fondamentali del sistema iperbolico

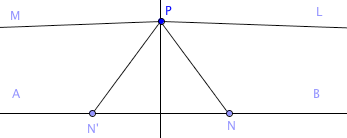
Passiamo ora ad alcuni concetti fondamentali di questa nuova geometria. Si considerino una retta AB e un punto P fuori di essa e si mandi per P la perpendicolare PO ad AB. Si prenda ora un altro punto N qualsiasi su AB. Se supponiamo che il punto N si allontani sulla retta nel verso, ad esempio che va da O verso B, si possono avere due casi:

 

a) N può ritornare al suo punto di partenza dopo aver percorso una distanza finita. Ciò corrisponde alla geometria non euclidea ellittica.

 

b) N può continuare a muoversi come sopra detto e la distanza ON tendere all’infinito, il che vale nella geometria ordinaria. La retta PN tende allora a una posizione limite definita PL e PL è detta essere parallela a OB (PL||OB). Ripetendo l’argomento per un punto N’ preso alla sinistra di O si giunge alla conclusione che PM||OA.

 

Ora nel caso b) si prospettano le due seguenti possibilità:

 

b1) Nell’ordinaria geometria euclidea le due semirette PL e PM costituiscono una sola retta, ossia gli angoli ^OPL e ^OPM sono entrambi retti.

 

b2) Nella geometria iperbolica invece si assume l’ipotesi che le due semirette PL e PM siano distinte e che i due angoli sopra detti siano acuti.

 

Poniamoci ora nel caso b2). Nella geometria iperbolica si avrà la seguente definizione: due rette PL e OB si dicono parallele quando sono complanari, non si incontrano se prolungate indefinitamente, mentre ogni semiretta condotta per P entro l’angolo ^LPO incontra la retta OB. Ne viene allora che data una qualunque retta AB, per un punto P fuori di essa si possono sempre condurre due parallele PL e PM tali che PL||OB e PM||OA.

 

Ci limitiamo a ricordare che nella geometria iperbolica la somma degli angoli interni di un triangolo risulta essere minore di due retti e, detta difetto di un triangolo la differenza D=  - A – B – C fra un angolo piatto e la somma degli angoli interni del triangolo, si ha che la superficie del triangolo è proporzionale al rispettivo difetto.